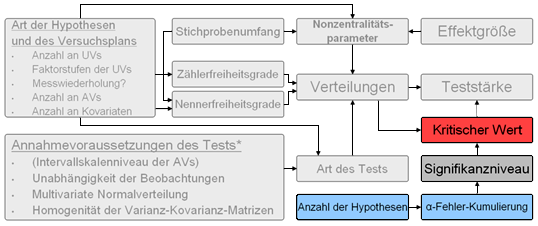
Weitere relevante Kenngrößen

Alphafehlerkumulierung I

Die Frage, wie viele Hypothesen in der Untersuchung gleichzeitig geprüft werden, beeinflusst die Teststärke der Untersuchung durch die Adjustierung des Alphaniveaus zur Vermeidung einer Alphafehlerkumulierung.

Das Phänomen der Alphafehlerkumulierung tritt grundsätzlich bei mehreren inferenzstatistischen Tests bzw. bei der Testung mehrerer Hypothesen auf. Es besagt, dass die Wahrscheinlichkeit, mit der ein postuliertes Muster in Zahlen gesehen wird, obwohl eigentlich keines oder ein anderes vorliegt, ansteigt, je häufiger die Zahlen "betrachtet" werden, d.h. inferenzstatistisch untersucht werden.

Als Beispiel kann man sich einen Würfelwurf vorstellen. Wenn man nur einmal würfelt, besteht nur einmal die Chance eine Sechs zu würfeln bzw. das Alphafehlerniveau zu überwinden. Wenn aber mehrfach gewürfelt wird, dann besitzt man gleich mehrere Chancen auf die Augenzahl Sechs und die Wahrscheinlichkeit, dass das festgelegte Niveau überwunden wird, steigt folglich an. Es beträgt nicht mehr 5%, sondern steigt wie folgt an:

π = 1 - (1 - α)^m

Hierbei gilt:
α = Signifikanzniveau (z.B. 5%)
m = Anzahl an Tests

In einer Studie sollen beispielsweise drei Hypothesen mit einem Signifikanzniveau von 5% getestet werden. Der tatsächliche Alphafehler läge hier bei 14.3%. Die Berechnung lautet:
π = 1 - (1 - 0.05)³ ≈ 0.143.

Die Alphafehlerkumulierung tritt nur dann auf, wenn die Tests unabhängig (orthogonal) voneinander sind. Wird beispielsweise zehn Mal derselbe Test angewandt, so führt dies nicht zu einem erhöhten Alphafehler.

Um dem Problem der Alphafehlerkumulierung zu begegnen, existieren verschiedene Korrekturverfahren. Diese stellen sicher, dass die Wahrscheinlichkeit in mindestens einem inferenzstatistischen Test ein Muster zu sehen, obwohl es überhaupt nicht existiert, nicht mehr als 5% beträgt. Eine Korrektur stellt die Ermittlung des neuen Signifikanzniveaus über die folgende Formel dar:

π = 1 - (1 - α)^1/m

Hierbei gilt:
α = Signifikanzniveau (z.B. 5%)
m = Anzahl an Tests

Als Korrekturverfahren zur Alphafehlerkumulierung kann man die Bonferroni-Korrektur mit folgender Formel verwenden:

Hierbei gilt:
α = Signifikanzniveau (z.B. 5%)
m = Anzahl der Tests

Besitzt eine Untersuchung mehrere Hypothesen, die man inferenzstatistisch überprüfen will, teilt man Alpha durch die Anzahl der Tests und verteilt damit die 5% auf die einzelnen Hypothesen. Somit wird das Signifikanzniveau von 5% insgesamt nicht überschritten.

In einer Untersuchung werden zum Beispiel drei Hypothesen getestet. Hierdurch ändert sich das 5%-Signifikanzniveau auf 5% : 3 = 1.67%. Demnach ist ein Alphaniveau von 1.67% für die Untersuchung zu wählen, wenn ein Signifikanzniveau von insgesamt 5% nicht überschritten werden soll.

Die Bonferroni-Korrektur stellt ein sehr einfaches Verfahren zur Korrektur der Alphafehlerkumulierung bereit. Als problematisch kann sich bei dem Verfahren die sehr konservative Testung erweisen. Dies bedeutet, dass fast nie Muster gesehen werden, d.h. die einzelnen Hypothesen haben sehr kleine (korrigierte) Alphaniveauwerte und können folglich kaum signifikant werden. Das Gegenteil einer zu konservativen Testung ist eine zu progressive Testung. In diesem Fall werden (zu) häufig Muster in den Zahlen gesehen.

Angenommen, eine Korrelationsstudie soll mit fünf Variablen für ein Konstrukt A und mit acht Variablen für ein Konstrukt B durchgeführt werden. Insgesamt werden in der Untersuchung 40 Korrelationen (5 ⋅ 8) ermittelt. Zur inferenzstatistischen Absicherung prüft man diese Korrelationen auf dem 5%-Niveau. Dabei kann die Bonferroni-Korrektur angewandt werden. Man erhält ein korrigiertes Alphaniveau von 0.125% (5% : 40). Diesen Wert muss eine einzelne Hypothese übertreffen, um Signifikanz zu erreichen. Formal zwar korrekt, aber möglicherweise viel zu konservativ.