Weitere relevante Kenngrößen

Nonzentralitätsparameter, zentrale und nonzentrale Verteilung

Zunächst werden folgende, für die Teststärke bzw. den Stichprobenumfang relevante Kennwerte besprochen:

• Signifikanzniveau
• Betaniveau
• Stichprobenumfang N
• Nonzentralitätsparameter λ
• Zentrale und nonzentrale Verteilung
• Teststärke bzw. Power (1 - β)

Da die meisten dieser Parameter bereits detailliert erörtert wurden, erfolgt an dieser Stelle lediglich eine Darstellung des Nonzentralitätsparameters sowie der zentralen und nonzentralen Verteilung.

Im univariaten Fall, d.h. bei einer abhängigen Variable, setzt sich der Nonzentralitätsparameter Lambda (λ) multiplikativ aus der Stichprobengröße N und der Effektgröße f² zusammen. Die Formel zur Berechnung des Nonzentralitätsparameters λ (für den F-Wert) lautet folglich:

λ = N ⋅ f²

Hierbei gilt:
λ = Nonzentralitätsparameter
N = Stichprobenumfang
f² = (angenommene) Effektgröße

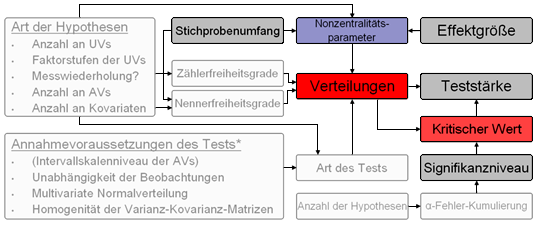
Die Verteilungen werden von dem Nonzentralitätsparameter λ, den Freiheitsgraden und der Art des Tests bestimmt. Der Nonzentralitätsparameter nimmt lediglich auf die nonzentrale Verteilung Einfluss, während die Zähler- und Nennerfreiheitsgrade sowohl die zentrale als auch die nonzentrale Verteilung maßgeblich festlegen. Die Art des verwendeten Tests legt fest, auf welche zentralen und nonzentralen Verteilungen (z.B. F-Verteilung, t-Verteilung, χ²-Verteilung usw.) zurückgegriffen wird.

Die F-Verteilung basiert auf F-Werten, die mit folgender Formel berechnet werden können:

Hierbei gilt:
F = F-Wert
QS_Zwischen = Hypothesenquadratsumme
QS_Innerhalb = Fehlerquadratsumme
df_Z = Zählerfreiheitsgrade
df_N = Nennerfreiheitsgrade

Die Hypothesenquadratsumme bezieht sich dabei auf die aufgeklärte Varianz, während die Fehlerquadratsumme auf die nicht aufgeklärte Varianz verweist. Summiert man die beiden Quadratsummen, so erhält man die totale Quadratsumme, welche die Gesamtvarianz repräsentiert. Die Zähler- und Nennerfreiheitsgrade werden im nächsten Abschnitt erörtert.